Número 366

 Dia 366 de 2024, 31 de dezembro

Número 29

Estamos perto do fim do 211.º dia de dois mil e vinte e quatro,  29.º de julho. 

Vinte e nove e duzentos e onze são números primos ou, dito de outro modo, números de prima importância, pois só há uma forma de os representar como um produto de dois números naturais:  1×29 e 1×211 respetivamente.

Tal como todos os restantes números ímpares, podem ser representados como soma de dois números naturais consecutivos, 14+15 e 105+106, mas por serem primos, não admitem mais nenhuma representação dessa natureza (soma de números naturais consecutivos). 

29 é um termo de um terno pitagórico primitivo (20, 21, 29), três medidas naturais de comprimento dos lados de um triângulo retângulo. Sabemos que o triângulo que tem estas medidas é retângulo porque é verdadeira a afirmação de que 20²+21²=29².

Número 176

 dia 176 de 2024 - 24 de junho

176 só tem uma representação como soma de números naturais consecutivos: uma escada de 11 degraus

______________________________

176 é o perímetro de um triângulo retângulo cujas medidas dos lados são números naturais e constituem um terno pitagórico primitivo (48, 55, 73).

Número 144

 Dia 144 de 2024  ―  23 de maio

Na imagem seguinte vê-se que

• 144 pode ser representado pela área de oito retângulos de dimensões naturais (inteiros positivos), um dos quais é quadrado ―144 é um quadrado perfeito ―, pelo que tem quinze divisores ou, também, 144 é múltiplo de quinze fatores;

• há dois triângulos retângulos com 144 de perímetro, cujo comprimento dos lados são números naturais; portanto estamos na presença de dois ternos pitagóricos; (36, 48, 60) e (16, 63, 65);

• 144 é o 12º termo da sequência de Fibonacci.

_______________________

Cento e quarenta e quatro escreve-se simbolicamente 144 no sistema de numeração decimal (de base 10) significando,

• 1 centena +  4 dezenas +  4 unidades
•  1 × 100    +  4 × 10        +  4 × 1
•  1 × 10²     +  4 × 10¹      +  4 × 10⁰

Enquanto soma de potências de base dois e expoente inteiro 144=128+16=2⁷+2⁴. Portanto, no sistema de numeração de base 2 escreve-se 10010000_(dois) significando,

1×2⁷ + 0×2⁶ + 0×2⁵ + 1×2⁴ + 0×2³ + 0×2² + 0×2¹ + 0×2⁰

 e 144 = 12² pelo que, na base 12 escreve-se 100_(doze) significando

1×12² + 0×12¹ + 0×12⁰    

_________________________

Como produto de números primos 144=2⁴×3² = 2×2×2×2×3×3

_________________________

144 pode ser decomposto diferentemente em 1728 somas de três parcelas, que corresponde a 12×144. Destas, apenas 432 (um quarto de 1728 e o triplo de 144) permitem construir triângulos (em virtude da desigualdade triangular); entre estes triângulos há dois que são retângulos (mostrados na imagem), 150 acutângulos, 280 obtusângulos. Isósceles são 35, entre os quais está um equilátero.

Triângulos perímetro = 144	Isósceles	Escalenos
Acutângulos	29*	121
Retângulos	0	2
Obtusângulos	6	274
	*1 equilátero

 ______________________

Uma vez que os retângulos (ou qualquer paralelogramo) têm os lados opostos iguais, o seu perímetro (P) é composto por dois comprimentos (C) e duas larguras (L), isto é, P= 2×(C+L). Se considerarmos retângulos com perímetro de 144 unidades de comprimento, o seu semiperímetro é 72. Encontrando todas as decomposições aditivas diferentes de 72 em duas parcelas (C+L) encontramos também todas as possibilidades de construir retângulos não congruentes de perímetro 144. Como 144 é múltiplo de 4, um desses retângulos será um quadrado. Queres ser tu a descobrir quantos são? Podes responder no comentário a esta publicação.

Número 140

 Dia 140 de 2024  ―  19 de maio

Cento e quarenta na base dez simbolicamente escreve-se 140 que significa 

• 1 centena    4 dezenas    0 unidades  
• 1 × 100        4 × 10           0 × 1
• 1 × 10²         4 × 10¹         0 × 10⁰ 

Enquanto soma de potências de base dois temos 128+8+4 = 2⁷+2³+2²

140 é um número par: pode ser representado pela área de um retângulo de 2 por 70 e também pelo perímetro de paralelogramos de medidas naturais, por exemplo, pelo quadrado de lado 35.

140 tem 12 divisores: 1 e 140, 2 e 70, 4 e 35, 5 e 28, 7 e 20, 10 e 14, ou seja, pode ser representado de seis formas diferentes como produto de dois fatores naturais. Com fatores primos 140 = 2×2×5×7. 

140 é um número piramidal, é a soma dos sete primeiros quadrados perfeitos: 1+4+9+16+25+36+49. Também pode ser escrito como soma de três quadrados perfeitos: 100+36+4.

140 é o perímetro de um triângulo retângulo cujos lados têm medidas inteiras (terno pitagórico 40, 42, 58) 40²+42²=58².

140 pode ser representado de três maneiras diferentes como soma de números naturais consecutivos (escadas numéricas): 

• 5 degraus: 26+27+28+29+30
• 7 degraus: 17+18+19+20+21+22+23
• 8 degraus: 14+15+16+17+18+19+20+21

Número 125

Dia 125 de 2024 - 4 de maio

125 tem quatro divisores {1, 125, 5, 25} tal como todos os cubos perfeitos de números primos.

_______________

125 é a medida da hipotenusa de um triângulo retângulo com lados de medidas naturais, pertencendo assim ao terno pitagórico (44, 117, 125); significa que 44²+117²=125²  

125 é também o quadrado da hipotenusa de dois triângulos retângulos, sendo, portanto, de dois modos diferentes, a soma de dois quadrados perfeitos: 

5² + 10² = 125 = 2² + 11² 

A raiz quadrada de 125 é pouco maior que 11.

_________________

Sendo um múltiplo de 5, tem uma escada de 5 degraus (soma de cinco números naturais consecutivos: 23+24+25+26+27) tal como 15 e todos os múltiplos de 5 superiores. Sendo múltiplo de 5 e não de 10, então tem uma escada de 10 degraus (figura seguinte) ao alcance de uma construção com material CUISENAIRE. 

E por ser um número ímpar tem uma escada de dois degraus 62+63 (ou será ímpar por ser soma de dois naturais consecutivos).

_________________

Representação binária:

1111101_(dois)

1 × 2⁶ + 1 × 2⁵ + 1 × 2⁴ + 1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰  

64 + 32 + 16 + 8 + 4 + 1

Número 50

 Hoje completam-se 50 anos após a Revolução dos Cravos. São 18263 dias vividos em democracia. 18263 dias perfazem exatamente 2609 semanas, pelo que estamos hoje numa 5.ª feira, tal como há 50 anos atrás.

50 é soma de quadrados perfeitos, 7² + 1² = 49 + 1 e de 5² + 5² = 25 + 25

Com isso podemos construir dois triângulos retângulos 'quase' interessantes: 

• o triângulo retângulo escaleno cujas medidas dos lados são 1, 7 e √50, 

• o triangulo retângulo isósceles com lados de medida 5, 5 e √50. 

√50 ≅ 7,071067... pouco mais que 7😉. Seria mais interessante se 50 também fosse um quadrado perfeito.

_________________

50 não é um número triangular, mas fica 'en/cravado' entre dois números triangulares, o 45 e o 55:

Conseguimos que 50 seja a soma de números triangulares, por exemplo, 10+10+15+15.

_________________

50 também é a soma dos quatro primeiros termos da sequência destas pirâmides:

A 4.ª pirâmide é formada pela soma dos quatro primeiros quadrados perfeitos, a 3.ª pirâmide é a soma dos três primeiros quadrados perfeitos, a 2.ª é a soma dos dois primeiros quadrados perfeitos e a 1.ª é o primeiro quadrado perfeito. 

_____________________________________

50 é metade de 10², tal como 5 é metade de 10¹, 500 é metade de 10³, . . . é bom saber, porque multiplicar um número N por 50 é o mesmo que pensar na metade de N × 100, ou seja,

N × 50 = N × 100 ÷ 2, assim como N × 5 = N × 10 ÷ 2, ou N × 500 = N × 1000 ÷ 2, e todos sabemos como é fácil pensar no produto de um número por 10, 100, 1000,... assim como é fácil pensar na metade de qualquer número, não? Também dividir N por 50 é o mesmo que pensar no dobro do quociente de N por 100. Contas fáceis.

O que não é tão fácil é multiplicar a democracia. 

Número 100

 Hoje é o dia 9 do mês de abril e é o dia 100 do ano 2024.

É possível construir cinco retângulos diferentes com 100 quadrados congruentes: 

Os divisores de 100 são 1 e 100, 2 e 50, 4 e 25, 5 e 20, e 10. 

A decomposição em fatores primos é 2²×5² que é igual ao produto de dois dos seus fatores 4×25. 

100 é um quadrado perfeito; é a soma dos quatro primeiros números cúbicos:

100 é o quadrado do 4.º número triangular, o qual é a soma dos quatro primeiros números naturais.

100 é a soma do quadrado de 8 com o quadrado de 6. Significa que há um triângulo retângulo com as medidas 6, 8 e 10 para os seus lados, sendo 10 a medida da hipotenusa.

No sistema de numeração de base oito, usando os algarismos 0, 1, 2, 3, 4, 5, 6, 7, cem escreve-se 144 (lê-se um, quatro, quatro na base oito). Ou seja  100 = 1 × 8² + 4 × 8¹ + 4 × 8⁰

Triângulos isoperimétricos

Há 833 decomposições de 100 em somas de três parcelas. Quantos triângulos de perímetro 100, com medidas inteiras, existem? Não há nenhum que seja equilátero porque 100 não é divisível por 3; mas o triângulo 33+33+34 fica muito perto disso.

Retângulos isoperimétricos

Com perímetro 100 e medidas inteiras é possível desenhar 25 retângulos, um deles é um quadrado de lado 25.

Número 30

De entre as 75 decomposições diferentes de 30 em somas de três parcelas de números naturais, há 18 que podem constituir-se como triângulos, sendo as medidas dos lados números inteiros. Desses 18 triângulos possíveis, 7 são isósceles e 11 são escalenos; dos que são isósceles há um que é equilátero (10+10+10), e dos escalenos destaca-se um que é retângulo (5+12+13).

 

Medidas dos lados			Quadrados dos lados
a	b	c	a2	b2	c2	a2+b2
10	10	10	100	100	100	200
2	14	14	4	196	196	200
4	13	13	16	169	169	185
6	12	12	36	144	144	180
8	8	14	64	64	196	128
8	11	11	64	121	121	185
9	9	12	81	81	144	162
4	12	14	16	144	196	160
5	11	14	25	121	196	146
6	10	14	36	100	196	136
6	11	13	36	121	169	157
7	9	14	49	81	196	130
7	10	13	49	100	169	149
7	11	12	49	121	144	170
8	9	13	64	81	169	145
8	10	12	64	100	144	164
9	10	11	81	100	121	181
5	12	13	25	144	169	169

Por permitirem construir um triângulo retângulo, 5, 12 e 13 são um "terno pitagórico" e 30 é o seu perímetro. Dentro do intervalo de dias num mês, para além do 30 há outros dois números que são perímetro de triângulos em é possível construir um triângulo retângulo: o 12 com o terno 3, 4, 5 e o 24 com o terno 6, 8, 10. 

Número 29

29 é um número primo. Vejamos um processo muito interessante para encontrar os primeiros números primos - o crivo de Eratóstenes - além de permitir identificar os números primos, ajuda a entender o que são.

29 é a hipotenusa de um triângulo retângulo com medidas inteiras no comprimento dos seus lados: 20 unidades de comprimento (u.c.) para o cateto menor, 21 para o segundo cateto e 29 para a hipotenusa.

Os números 20, 21 e 29 são um terno pitagórico, i.e., três números inteiros que verificam a igualdade no teorema de Pitágoras: 20²+21²=29².

Número 17

 

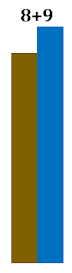
8+9 é a escada de 2 degraus do 17 17 é um número primo porque só possui uma escada, que tem apenas 2 degraus (o 2 é uma exceção, é primo mas não tem escada)   17 é número ímpar pois é soma de dois números consecutivos Outras decomposições destacando o 10 10 + 7        10 + 6+1          10 + 1+6 10 + 5+2          10 + 2+5 10 + 4+3          10 + 3+4